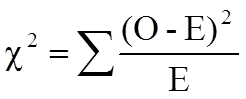
In order to be a confounder, the extraneous factor must be associated with the primary exposure of interest and also be associated with the outcome. One approach would be to test these associations using a test of hypothesis. Our primary interest was in the association between obesity and CVD, but we were also concerned that age might be a confounding factor. We could use a χ2 test to test 1) whether there is an association between age and obesity and 2) whether age is associated with CVD.
The formula for the test statistic is
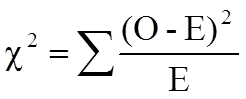
The condition for appropriate use of the above test statistic is that each expected frequency is 5 or more. In Step 4 we will compute the expected frequencies and ensure that the condition is met.
The data for testing the association between age and obesity are shown in the table below. The numbers in parentheses indicate the expected values under the null hypothesis (no difference in frequency obesity for those age<50 and those age50+).
|
|
Obese |
Not Obese |
Total |
| Age < 50 |
100 (180) |
500 (420) |
600 |
| Age 50+ |
200 (120) |
200 (280) |
400 |
| Total |
300 |
700 |
1000 |
From these data, χ2 = 35.56 + 15.23 + 53.33 + 22.86 = 126.98.
There are two rows and two columns, so the degrees of freedom = (2-1)(2-1)=1(1)=1. For df=1 and a 5% level of significance, the critical value is 3.84, so we will reject H0 if χ2 > 3.84. Therefore, we reject H0 because 126.98 > 3.84. We have statistically significant evidence at a=0.05 to show that H0 is false; age and obesity are not independent (i.e., they are related). The p-value is p < 0.005.
We can use the same procedure to assess whether age is associated with incident CVD. The data for this association are shown below, with the values expected for the null hypothesis shown in parentheses.
|
|
Incident CVD |
No CVD |
Total |
| Age < 50 |
45 (63.6) |
555 (536.4) |
600 |
| Age 50+ |
65 (42.4) |
335 (357.6) |
400 |
| Total |
110 |
890 |
1000 |
For this association, χ2 = 5.44 + 0.64 + 8.16 + 0.97 = 15.21.
Once again, df=(2-1)(2-1)=1(1)=1. For df=1 and a 5% level of significance, so we reject H0 because χ2 > 3.84.
Because age is related to obesity (17% of younger persons are obese as compared to 50% of older persons, and 67% of obese persons are 50 years of age and older as compared to 29% of non-obese persons) and age is related to incident CVD (7.5% of younger persons developed CVD as compared to 15.3% of older persons), age is a confounder. Therefore, some of the association between obesity and incident CVD can be attributed to age.